Schnellzugriffe
Follow @HvGG_eduMeistgelesen
Aufgabe des Monats Oktober 2018
- Letzte Änderung:
- 23.09.2018
- Verantwortliche/r:
- Rainer Durdaut
Aufgabe des Monats Oktober 2018
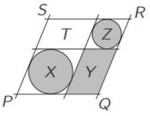
Drei Parallelen werden von drei anderen Parallelen so geschnitten, dass, wie im Bild, in zwei der entstehenden Parallelogramme Kreise einbeschrieben werden können. Die Flächeninhalte der grauen Flächen seien X, Y und Z, der des Parallelogramms PQRS sei W, und der des weißen Parallelogramms sei T. Wie viele von den Werten X, Y, Z, W muss man mindestens kennen, um T zu bestimmen? Auch dieses Mal gibt es wieder wertvolle N.E.R.D.-Punkte zu gewinnen.
Lösung: Es reicht, Y zu kennen, denn es gilt T=Y. Zu T und Y gehören zwei Parallelogramme, bei denen alle Seiten und ein Winkel gleich sind. Die Parallelogramme sind also kongruent und haben denselben Flächeninhalt.
Auch dieses Mal gab es sehr unterschiedliche und kreative Beweise. Eine Schülerin hat die Gleichheit über trigonometrische Funktionen gezeigt, ein Schüler wählte einen Ansatz über die Strahlensätze. Besonders konzis und elegant war die Erkenntnis, dass ein Parallelogramm mit Inkreis eine Raute ist, woraus direkt die Gleichheit entsprechender Seiten der zu Y und T gehörigen Parallelogramme folgt.
Auch folgende Argumentation führt zum Ziel. Schert man das äußere große und damit natürlich auch die inneren Parallelogramme, so bleiben die Flächeninhalte gleich. Die Durchmesser der in den Rechtecken liegenden Kreise liefern direkt den Beweis.
Allen Einsendern sei für ihre rege und einfallsreiche Beteiligung gedankt.